In rechthoekige driehoeken is het vierkant vanuit de zijde die onder de rechte hoek ligt gelijk aan de vierkanten vanuit de zijden die de rechte hoek omvatten.
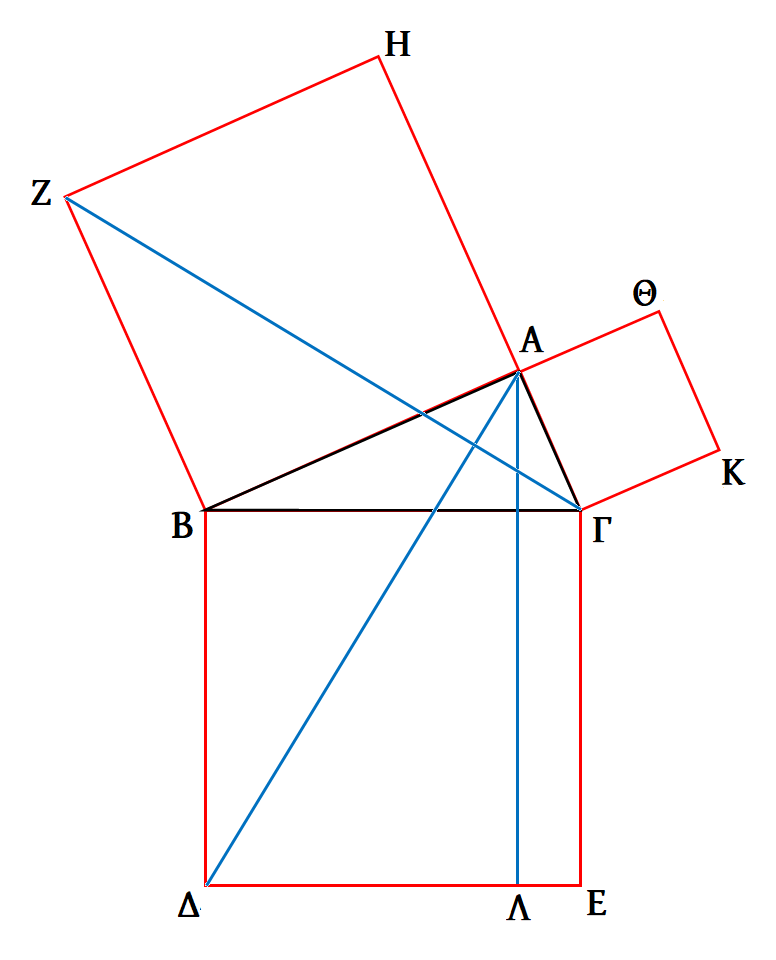
Laat er een rechthoekige driehoek ΑΒΓ zijn die de hoek ΒΑΓ recht heeft. Ik zeg dat het vierkant vanuit ΒΓ gelijk is aan de vierkanten vanuit ΒΑ en ΑΓ. Laat namelijk vanuit ΒΓ het vierkant ΒΔΕΓ getekend worden, en vanuit ΒΑ en ΑΓ de vierkanten ΗΒ en ΘΓ. En laat door A parallel aan één van beide, ΒΔ of ΓΕ, de lijn ΑΛ getrokken worden. En laat ΑΔ en ΖΓ verbonden zijn.
[…]
En het parallellogram ΒΛ is het dubbele van de driehoek ΑΒΔ, want ze hebben dezelfde basis ΒΔ en bevinden zich tussen dezelfde parallelle lijnen ΒΔ en ΑΛ. En het vierkant ΗΒ is het dubbele van de driehoek ΖΒΓ, want zij hebben weer dezelfde basis ΖΒ en bevinden zich tussen dezelfde parallelle lijnen ΖΒ en ΗΓ. En tweevouden van gelijke zaken zijn gelijk aan elkaar, dus is het parallellogram ΒΛ ook gelijk aan het vierkant ΗΒ.
[…]
Dus in rechthoekige driehoeken is het vierkant vanuit de zijde die onder de rechte hoek ligt gelijk aan de vierkanten vanuit de zijden die de rechte hoek omvatten, wat aangetoond moest worden (QED).